
Tamaño muestral
En este artículo voy a responder la pregunta que más me hacen mis clientes: ¿qué muestra debo tomar para que los resultados de la encuesta sean representativos?
Este es un aspecto clave para realizar una investigación de mercados.
Hay otros muy importantes, obvio. Pero este es el primero que se plantea todo el mundo, pues a mayor tamaño de muestra, más presupuesto va a ser necesario destinar.
Por lo tanto, es fundamental ser capaz de calcular cuál es el tamaño de muestra mínimo que me vaya a dar resultados fiables y útiles. Pero ojo, porque la representatividad no sólo es cuestión de números; se necesita método para que realmente la muestra que logremos sea un reflejo adecuado de la realidad. Sin embargo, de eso hablaremos en otro momento.
Así que, volviendo al método para calcular una muestra representativa, te diré que sólo requiere tener en cuenta 4 variables…
…y un invitado de última hora que muchas veces provoca que, después de haber hecho todos los cálculos de forma metódica, la representatividad de los resultados falle estrepitosamente.
Vamos primero con las 4 variables que todo el mundo conoce y luego desvelamos ese intruso que puede dar al traste con la validez de los resultados obtenidos en la investigación de mercados.
A la hora de determinar el número de “encuestas necesarias” o tamaño de una muestra para un estudio cuantitativo, es importante conocer el tamaño del universo.
El universo hace referencia al total de individuos que componen el colectivo a investigar. Por ejemplo, si son votantes, el universo serían todas las personas mayores de 18 años con derecho a voto. Si el estudio es sobre hombres zurdos de una provincia, pues todos los que cumplan dicha condición, etc. Intuitivamente es fácil suponer que contra más grande es el universo, más encuestas necesitaremos. Sin embargo, eso no es del todo cierto… Veámoslo con otro ejemplo. Muy insignificante, cierto es. Pero verás que así se comprende mejor.
Imaginemos que 3 personas han entrado en un hotel y en la recepción han dejado su DNI: 2 son mujeres y 1 es un hombre. Objetivo: queremos analizar los DNI para conocer más de nuestros clientes, pero no tenemos mucho tiempo. Así que a alguien se le ocurre que podemos sacar una muestra. La analizaremos y si en la muestra todo va bien, habremos reducido el tiempo dedicado a la tarea en una tercera parte.
Parece un gran plan, ¿cierto? Pues veamos qué ocurre…
Nos ponemos manos a la obra. Decidimos que la muestra a analizar es de 2 documentos.
Caray: 2 de 3.
Eso implica que la muestra supone dos terceras partes del universo: ¿qué encuesta tiene tanta representatividad? ¡Una muestra del 66% nada menos!
Pero… al analizar los 2 documentos puede suceder que:
- 1 sea de mujer y otro de hombre.
- Los 2 sean de mujer.
Así que, en ambos casos, para estimar el sexo de las personas estaríamos cometiendo un considerable error:
- En el primer ejemplo, sobreestimaríamos los hombres e infrarrepresentaríamos a las mujeres en un 16,7%.
- En el segundo caso, sobreestimaríamos a las mujeres e infrarrepresentaríamos a los hombres en un 33,3%.
La segunda muestra sería la peor, pero como esto es azar, no sabemos cuál nos tocaría…
En conclusión: cuando los universos son pequeños, necesitamos muestras proporcionalmente mayores. Por contra, cuando el universo pasa de los 50.000 efectivos, podemos considerarlo infinito, y ahí, por mucho que incrementemos la muestra, apenas mejora el margen de error.
En términos técnicos el error muestral es el error que cometemos por el hecho de generalizar datos de una muestra y no contar con el dato de todo el universo o colectivo objeto de estudio. Es decir, como trabajamos con muestras ya sabemos que hay cierta probabilidad de que las conclusiones obtenidas de su análisis no sean 100% extrapolables a lo que ocurre en el universo. Así que la cuestión es tener controlado ese error. Saber cuánto nos estamos equivocando.
Y en realidad de esto va la pregunta: “¿cuántas encuestas necesito?”.
De modo que vamos al meollo de la cuestión y veamos qué es eso del margen de error.
Aclarémoslo con otro ejemplo: imaginemos que vamos a una feria en la que existe una atracción de lanzamiento de hachas. Si aciertas arrojando el hacha sobre el centro de la diana, te llevas el osito de peluche. A nadie se le escapa que, si el blanco es pequeño, la probabilidad de llevarle el osito a tu sobrina pequeña y que ella te quiera eternamente … es tendente a nula. Para elevar esa probabilidad tenemos que contar con un cierto margen de error: que el blanco sea más grande. Así que, a mayor margen de error o tamaño de la diana, mayor probabilidad de acertar o nivel de confianza.
Un 5% de margen de error suele ser considerado aceptable en investigación social.
Atenta a este dato porque causa confusión.
Normal por otra parte, porque en los estudios de mercado es habitual diseñar encuestas con un margen de error del 5% y un nivel de confianza del 95%.
Así que el cálculo que nos invita a hacer el desconocimiento sobre estadística es: 5% + 95% = 100%.
Y no es así.
De hecho, se suele trabajar con un nivel de confianza del 95% o del 97,5%. Es decir, una probabilidad de acertar del 95% o del 97,5%. ¿Cuál usar? Eso va de gustos, o de necesidades puntuales, aunque tratándose de encuestas, no tendrá mucha incidencia.
Por insistir una vez más, el nivel de confianza tiene una relación directa con el margen de error, pero no suman 100 entre ambos porque son dos cosas diferentes y no se pueden sumar.
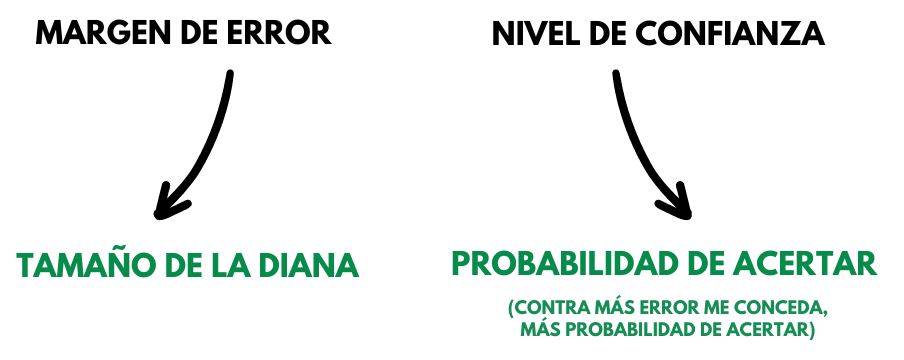
El nivel de confianza es la probabilidad de acertar cuando generalizamos un dato de una muestra al conjunto del universo. Como en la quiniela: si te concedes más margen de error poniendo un resultado triple en un partido que te causa dudas, tienes mucho más nivel de confianza en que puedes lograr el pleno al 15.
Además de las 3 variables vistas hasta ahora, para calcular el tamaño de muestra perfecto, tenemos que considerar la heterogeneidad del colectivo a estudiar.
¿Heteroqué?
Heterogeneidad o variabilidad.
Que en lenguaje de calle sería como decir “necesito saber cómo de diferentes entre sí son los individuos del universo”.
Supongamos que queremos realizar un estudio sobre hábitos religiosos.
- Si el universo objeto de estudio es una congregación religiosa que vive en un convento de clausura, a nadie se le escapa que por muy grande que sea el universo, con una muestra muy muy pequeña podremos obtener información relevante de sus hábitos (porque todos los integrantes de la congregación, poco más o menos, tendrán las mismas costumbres).
- Si queremos estudiar los hábitos religiosos en un espacio en el que conviven dos religiones y la mitad de la población profesa una religión y la otra mitad la otra, parece claro que necesitaremos una muestra mucho más amplia si queremos obtener resultados concluyentes.

Pero de esto de la desviación típica ya hablamos otro día en mayor profundidad.
Para cerrar este punto, añadir que, si no sabemos nada del universo, asumimos que la población es totalmente heterogénea. Una medida de cautela …por si acaso. Esto se representa con la expresión pq=0,5 o lo que es lo mismo: la probabilidad de que cada persona de la muestra tenga una característica (p) es de 0,5 y la probabilidad de que no la tenga (q), de otro 0,5. Por el contrario, si p=0,9 y q=1 querría decir que el público de la encuesta es muy parecido: el 90 % (p=0,9) tienen esa característica (por ejemplo, están satisfechos con tus servicios) y el 10% (q=0,1) no lo están. Si se da está circunstancia, no necesitas hacer tantas encuestas, porque como ya hemos dicho…tus clientes son razonablemente parecidos al menos en cuanto a satisfacción con tus servicios.
Pues ya que estamos… aprovechemos e introduzcamos algunas preguntas más en la encuesta.
Así la rentabilizamos.
A priori tiene sentido.
Y sin embargo, este pequeño detalle da al traste con la representatividad de los resultados conseguidos con cierto tamaño de muestra.
Lo vemos con otro ejemplo:
Imagina que quieres realizar una encuesta en una ciudad para conocer cuántas personas están buscando una vivienda. Supongamos que en la ciudad viven 300.000 personas, y que queremos cometer un error máximo del 5% para un nivel de confianza del 95%. Por estudios anteriores sabemos que el porcentaje de personas que buscan vivienda en un momento puntual suele ser de entre el 4% aunque puede variar. Y eso es precisamente lo que queremos medir. Con estos datos podemos asumir que la población es muy homogénea respecto al objeto de estudio (comprarán vivienda p0,04 y no lo harán q 0,96) y eso significa que no necesitamos una muestra muy grande: todos son muy parecidos, de hecho, la mayoría no comprarán vivienda.
Sin embargo… a alguien se le ocurre que pues ya que estamos haciendo la encuesta… a las personas que digan que buscan vivienda, vamos a preguntarles qué buscan en concreto: un chalet, un apartamento, un ático, un piso de 4 habitaciones, etc.
Si hemos seleccionado una muestra de 400 individuos, que cubre con creces los objetivos anteriores, nos encontraremos con aproximadamente 16 personas que estén buscando vivienda (4% de 400). Y con 16 encuestas, tratar de representar a un colectivo de aproximadamente 15.000 personas (5% de 300.000), si suponemos que son muy heterogéneos en sus deseos de tipo de vivienda, estaremos cometiendo un error del 21,9%…
¿Cómo hemos calculado el error? Hemos aplicado la formula del error muestral para estimar la proporción de personas que comprarían vivienda de un tipo u otro asumiendo que:
- Queremos tener una probabilidad de acertar del 95% (que en la formula se identifica con la puntuación z=1,96)
- Que son datos totalmente heterogéneos (p y q =0,5 como ya hemos visto antes)
- La población objeto de estudio es infinita
- La muestra obtenida es 16
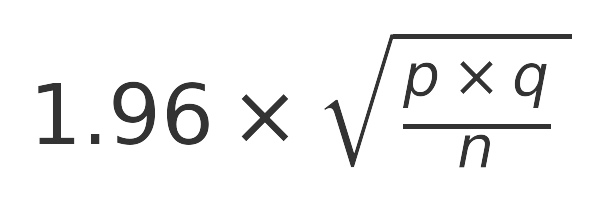
O lo que es lo mismo…
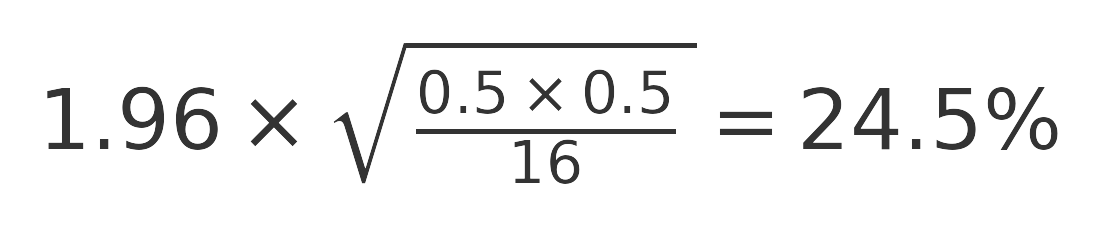
Pero si no quieres hacerlo, accede aquí a nuestra calculadora de tamaño de muestras y error muestral.
Por tanto, en el ejemplo que nos ocupa, si vamos a necesitar profundizar en algún colectivo, tendremos que preverlo previamente en el diseño de la muestra.
O nos llevaremos grandes sorpresas.
Y no agradables precisamente…
Resumiendo…
Para responder a la pregunta sobre cuál es el tamaño necesario de una muestra para que resulte representativa y sus resultados concluyentes, debemos tener en cuenta:
- El tamaño del universo. Si no lo conoces con precisión, considera que es un universo infinito (más de 50.000 individuos).
- El margen de error y nivel de confianza tolerable en el estudio. (Margen de error del 5% y nivel de confianza del 95% es una buena referencia).
- La heterogeneidad del universo. Si no la conoces, asume pq=0,5.
- Y no pierdas de vista los pues ya que estamos. Esto es; debemos prever si vamos a necesitar profundizar o no en determinados segmentos, para que la muestra sea suficientemente representativa en cada uno de ellos.
Pero lo que con más frecuencia olvidamos, lo que a veces no tenemos en cuenta …es que esto no sólo va de números. No sólo debemos garantizar una muestra suficiente. Todo lo dicho no sirve de nada si no podemos garantizar un muestreo aleatorio. Si introducimos sesgos al encuestar, da lo mismo el número de encuestas. Si hacemos encuestas a 1500 amigos, tendremos una buena muestra de amigos, podremos pero ¿realmente representan al público objeto de estudio?
Regla general. Tamaño de muestra “universal”
Si has visto alguna vez informes estadísticos, pero no eres experto en la materia igual te ha parecido curioso que muchos de ellos utilicen un tamaño de muestra de 400 individuos.
Te explico ahora de dónde sale ese numerito.
Si partimos de estas cuatro premisas:
- Universo infinito.
- Margen de error del 5%.
- Nivel de confianza del 95%.
- Heterogeneidad máxima (pq=0,5).
Y asumimos que no necesitamos profundizar en los diferentes subgrupos, entonces aplicamos la fórmula correspondiente para el cálculo de muestras aleatorias, y concluimos que necesitamos 384 encuestas.
Esta es la fórmula que utilizaríamos:

Donde:
- σ = Nivel de confianza (95% o 99%)
- p = Heterogeneidad o probabilidad de que la población tenga esa característica (0,5 si no la conocemos)
- e = Margen de error expresado en tantos por uno ( 0,05 sería ±5%)
Para que no tengas que resolver ecuaciones, en nuestra web puedes encontrar una herramienta que hace estos cálculos por ti una vez que los introduzcas.






